三角関数の加法定理(かほうていり)とは、三角関数どうしの加法(足し算)と減法(引き算)に関する定理である。
符号は全て複号同順。±と∓は上なら上、下なら下で等号が成り立つ。



cot, sec, csc に関する式は以下の通り。あまりきれいな形にはならず、エンペディア読者にこれらを使う人はあまりいないと思われるが、鉄道分岐器に使うので参考までに記載しておく。



倍角公式[編集]
加法定理から、以下の公式が簡単に導出できる。
2倍角の公式[編集]
y = x と代入し整理するだけで以下の公式が導かれる。



3倍角の公式[編集]
y = 2x とし、さらに2倍角の公式も用いて整理することにより以下の公式が導かれる。



同様に 4倍角の公式、5倍角の公式、…… なども導けるが、導出が簡単なうえに使用する場面はほとんどないため、覚える必要はほとんどない。
計算問題で sin7x や cos7x を含む数式を見ても「7倍角の公式なんて知らない!無理!(>_<)」などと慌てる必要はない。倍角公式を使わない別の方法がきっとあるはずである。
半角公式[編集]
2倍角の公式より、 cos 2x を sin2 x , cos2 x , tan2 x のみで表すことができることから、 2x を x と置きなおして整理することにより以下の公式が得られる。



和積公式[編集]




これをうまく変形すると得られる。




覚え方[編集]
sinとcosに関する2つの式については、以下の覚え方が有名である。
- 咲いたコスモス コスモス咲いた
- コスモスコスモス 咲かない咲かない
sinを「咲く」、cosを「コスモス」、符号が逆になる部分を「ない」で表現している。
これ以外にも覚え方はたくさんある。sinとcosを別の文字列に置き換えるものが多く、小林(cos)幸子(sin)や埼玉県(sin)越谷市(cos)が登場したり、死んだり(sin)殺したり(cos)、性的表現をふんだんに使用したりとバリエーションは尽きない模様[1]。あと、「しんこすこすしん、こすこすしんしん」という力技の覚え方もある。[2]
3倍角のsinについては、「3番三振、4番3三振」と覚えることも可能である。
ここでは高校の教科書に載っている一般的な方法で証明を行う。まず余弦定理を用いて  に関する式を証明し、三角関数の相互関係より他の式も導く。
に関する式を証明し、三角関数の相互関係より他の式も導く。
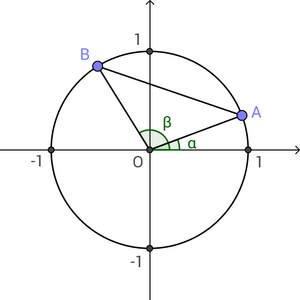
単位円上に2点  をとる。2点間の距離の公式より、
をとる。2点間の距離の公式より、

三角形OABに余弦定理を用いると、

以上の2式を等号で結び、さらに整理すると以下の式が得られる。

ここで、  または
または  であるが、
であるが、  であるため、どちらの場合でも
であるため、どちらの場合でも  が成り立つ。よって、
が成り立つ。よって、

(1)式と三角関数の関係式より、その他の加法定理の公式も導ける。(複号は同順とする)



複素数と絡めた解釈[編集]
高校数学の範囲外だが、オイラーの公式  を使うと、加法定理は指数法則に従い、容易に導き出せる。
を使うと、加法定理は指数法則に従い、容易に導き出せる。

より、実部と虚部を取れば導くことができる。
- ↑ これに限らず、数学は何かしらの覚え方をマスターしておくべきである。(私論)
- ↑ この場合、tanについても「いちひくたんたんたんたすたん」と覚えられる。
関連項目[編集]