よみもの:恒星までの距離を求める

	よみものページ
	この「よみもの」は、あんだくが作成したものです。 他ユーザーの編集も歓迎いたします。

そこらへんの恒星までの距離を、高校地学までの学習範囲で求めてみよう。

年周視差の利用

年周視差

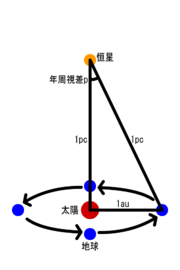
地球は太陽を中心に公転しているが、その公転の半径、すなわち地球と太陽の間の距離を1天文単位とよび、1auと表す。また、地球の公転軸上の恒星を太陽から見たときと太陽から1au離れた地球から見たときに見える角度の差(視差)を、地球の公転によって1年間かけてその状態が変化し元に戻るため、その恒星の年周視差と呼び、parallaxの頭文字をとりpと表す。
ある恒星の年周視差が1"のとき、その恒星から太陽までの距離を1パーセクとよび、1pcと表す。このとき、1"はきわめて小さいのでその恒星から地球までの距離も1pcであるといえる。
ここで 1au≒1億4960万km より 1pc≒3.26光年 であり、ある恒星までの距離dは年周視差pに反比例するので以下の式が得られる。

$d={\frac {1}{p}}pc={\frac {3.26}{p}}$光年

ある恒星の年周視差が分かれば、この式を用いることでその恒星までの距離を求めることが出来る。

練習問題 : 年周視差の利用

おおいぬ座シリウスAの年周視差は約0.379"である。地球からシリウスAまでの距離dをパーセクで求めよ。また、光年で求めよ。

解答と解説は右をクリックして表示！

年周視差p=0.379" より、 $d={\frac {1}{0.379}}=2.638...=2.64pc$ (答) また 1pc=3.26光年 より、 $d=3.26\times 2.638=8.599...=8.60$光年 (答)

年周視差さえわかれば上記のような簡単な計算をするだけでその恒星までの距離を求めることが便利である。一方で、年周視差で恒星までの距離を求めることには、想像にも難くないが、恒星までの距離dと年周視差pが反比例するから遠い恒星であれば年周視差が測定できず距離が求められない、という欠点がある。

分光視差の利用

HR図(ヘルツシュプルング・ラッセル図)

年周視差を利用しても求められない距離の恒星までの距離を求めるときには分光視差を用いよう。
恒星などの天体の明るさを表すとき、等級を用いることが多いが、地球上からその天体を見たときの明るさを見かけの等級または実視等級とよび、その天体を地球から10pcの距離においたときの明るさを絶対等級とよぶ。そして、ある恒星の見かけの等級と絶対等級の差からその恒星までの距離を求めるのが分光視差の利用で、分光視差法とよぶ。 等級の値が小さいほどその天体は明るく、等級が5上がると100倍明るくなる、即ち等級が1上がるごとに${\sqrt[{5}]{100}}$倍明るくなる。
分光視差を利用するにはその恒星の見かけの等級と絶対等級を知っておく必要がある。
見かけの等級は観測により分かる。
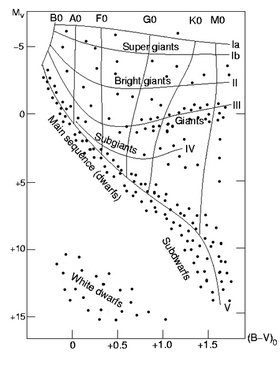
絶対等級は、その恒星のスペクトル型がわかればHR図(ヘルツシュプルング・ラッセル図)から簡単に求められる。スペクトル型とは光をスペクトル分解したときの状態の種類のことである。また、HR図は横軸にスペクトル型、縦軸に絶対等級をとったものであり、図中左下の星の集まりは白色矮星、左上から右下にかけての帯状の星の集まりは主系列星、右上の星の集まりを巨星である。

分光視差の利用

見かけの等級と絶対等級がわかったら実際に分光視差法にのっとって恒星までの距離を求めてみよう。
はじめに、求める恒星の見かけの等級をm等級、絶対等級をM等級とおく。このとき、2つの等級の差 $m-M$ を距離指数とよぶ。また、上にも述べたが、1上がるごとに${\sqrt[{5}]{100}}$倍明るくなるから、等級が $m-M$ 大きくなると ${\sqrt[{5}]{100}}^{m-M}$ 倍暗くなる。 ここで、恒星の見かけの明るさは距離の2乗に反比例する(たとえば、距離が2倍になると見かけの明るさは${\frac {1}{4}}$倍になる)から、絶対等級のときの距離に対する実際の距離の割合を$D$とおくと、

$D^{2}\times {\frac {1}{{\sqrt[{5}]{100}}^{m-M}}}=1^{2}\times 1$

である。
絶対等級のときの距離は10pcだから、この恒星までの距離を$d$pcとおくと

$d=10D$

の式が得られる。

練習問題 : 分光視差の利用 (1)

ほうおう座ζAは見かけの等級が 3.9 でスペクトル型が B6V である。HR図によるとスペクトル型が B6V であるときの絶対等級が -0.9 であるとき、この恒星までの距離を光年で求めよ。ただし、${\sqrt[{5}]{100}}=2.51$とする。

解答と解説は右をクリックして表示！

HR図の情報により、この恒星のスペクトル型が B6V より、この恒星の絶対等級は -0.9 である。このとき、この恒星の距離指数は $3.9-(-0.9)=4.8$ より 4.8 。 したがって、この恒星は絶対等級の位置のときよりも $2.51^{4.8}=82.87...=82.9$ より82.9倍暗い。 ここで、恒星の見かけの明るさは距離の2乗に反比例するから、絶対等級のときの距離に対する実際の距離の割合を$D$とおくと、 $d^{2}\times 1=1^{2}\times 82.9$ より、$D=9.10$ ここで、絶対等級のときの距離は10pcだから、この恒星までの距離を$d$pcとおくと、 ${\begin{aligned}d&=10D\\&=10\times 9.10\\&=91.0\\\end{aligned}}$ 1pc=3.26光年 より、求める距離は $91.0pc\times 3.26=296.6...=297$光年 (答)

なお、実際に分光視差を利用する場合には簡略化して次の式を用いることが多い。

$M=m-5\log _{10}d+5$

この式で、Mは絶対等級、mは相対等級、dパーセクは恒星までの距離をそれぞれ表している。

練習問題 : 分光視差の利用 (2)

へびつかい座70Aは見かけの等級が 4.03 でスペクトル型が K0V である。HR図によるとスペクトル型が K0Vである時の絶対等級が 5.5であるとき、この恒星までの距離を光年で求めよ。

解答と解説は右をクリックして表示！

HR図の情報により、この恒星のスペクトル型が K0V より、この恒星の絶対等級は 5.5 である。 恒星までの距離を$d$pcとおき、絶対等級と見かけの等級と恒星までの距離の関係式を用いて $5.5=4.03-5\log _{10}d+5$ これを解いて$d=5.08$ 1pc=3.26光年 より、求める距離は $5.08pc\times 3.26=16.56...=16.6$光年 (答)

セファイドの利用

年周視差を利用できないときには分光視差を利用すればよかったが、距離が遠くなるとHR図でスペクトル型から絶対等級を導き出すことができなくなる。そんな場合にはセファイドを用いることになる。
明るさが変化する星を変光星という。そして、変光星の中でも星自体が膨張と縮小の脈動を繰り返すことで明るさが変化するものを脈動変光星とよぶ。さらに、脈動変光星の中でも変光周期と絶対等級の間に正比例関係があるものをセファイド、またはケフェウス型変光星とよび、セファイドにおける変光周期と絶対光度の関係を周期光度関係とよぶ。
ある星団や銀河までの距離を求めるときにその内部のセファイドの変光周期が分かれば周期光度関係を用いて絶対等級がわかる。絶対等級がわかったら見かけの等級と比較することでその星団や銀河までの距離を求めることができる。
ある恒星までの距離を求めたいときにはその恒星を含む星団や銀河のセファイドからその星団や銀河までの距離を出せば、ざっくりとその恒星までの距離が分かることになる。

ハッブルの法則の利用

赤方偏移

分光視差もセファイドも利用できない遠くの銀河の場合には、宇宙の膨張の理論を利用することになる。
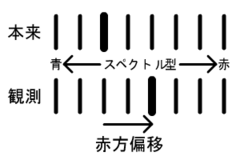
ほぼすべての銀河から届く光はスペクトルの分解をするとその暗線(吸収線、フラウンホーファー線)が本来よりも赤い、すなわち波長の長い方に移動している。これを赤方偏移という。本来波長λのスペクトル線がΔλだけ長く観測されたとき、赤方偏移zは以下のように計算で求められる。

$z={\frac {\Delta \lambda }{\lambda }}$

赤方偏移は光の波長が長くなって光のドップラー効果が発生したために起こる現象であり、光の波長が長くなった(=光のドップラー効果がおこった)のはその銀河が我々から遠ざかっているからである。このとき、銀河が我々から遠ざかる速度を後退速度という。

宇宙の膨張の様子

銀河が我々から遠ざかっているのは宇宙が膨張しているからである。宇宙は膨張しているが、これは右の図のように銀河が大きさを変えないで空間だけが膨張している状態である。このとき、地球を含む銀河(銀河系)から我々が宇宙を見たときほぼすべての銀河は銀河系からも遠ざかっていて、さらに遠くの銀河ほど早く遠ざかっている(後退速度が大きい)ことになる。
遠くの銀河ほど後退速度が速いため、赤方偏移も大きく、後退速度vは赤方偏移zが1よりもかなり小さいとき光速cを用いて

$v=cz$

であらわされる。なお v=c のときその銀河は光速で我々から遠ざかっていることになるのでそこから発せられた光は永久に我々のもとには届かない。
ここまで、遠くの銀河ほど後退速度が大きい、と述べてきたが、実を言えば銀河までの距離rと後退速度vは比例の関係にあり(ハッブルの法則)、以下の式であらわされる。

$v=Hr$

ここで、比例定数Hをハッブル定数とよび、その値はおよそ H=72(km/s)/Mpc である。ここで、Mpcはメガパーセクと読み 1Mpc=10⁶pc である。

練習問題 : 赤方偏移とハッブルの法則の利用

ある銀河のスペクトルのある暗線が、本来なら 0.400μm にあるところ 0.428μm のところに観察された。この銀河団までの距離をメガパーセクで求めよ。ただし、光速 $c=3.0\times 10^{5}$km/s 、ハッブル定数 $H=70$(km/s)Mpc とする。

解答と解説は右をクリックして表示！

本来の波長を $\lambda$μm 、観測された波長と本来の波長の差を $\Delta \lambda$μm とすると、 ${\begin{array}{lcl}\lambda &=&0.400\\\Delta \lambda &=&0.428-0.400=0.028\end{array}}$ 従って、赤方偏移 $z$ は、 ${\begin{aligned}z&={\frac {\Delta \lambda }{\lambda }}\\&={\frac {0.028}{0.400}}\\&=0.07\\\end{aligned}}$ よって、後退速度 $v$km/s は、 ${\begin{aligned}v&=cz\\&=3.0\times 10^{5}\times 0.07\\&=21000\\\end{aligned}}$ したがって、ハッブルの法則より求める距離 $r$Mpc は $v=Hr$ ${\begin{aligned}r&={\frac {v}{H}}\\&={\frac {21000}{70}}\\&=300\\\end{aligned}}$ よって、$300$Mpc (答)