|
よみものページ
|
この「よみもの」は、Imuzakが作成したものです。
他ユーザーの編集も歓迎いたします。
|
音を物理的に定義し、ついでに音速を計算してみましょう。
使うもの[編集]
参考になりそうなwebページにリンクしてあります。
- 高校レベルの数学の知識(公式をたくさん暗記する必要はない)
- 偏微分の知識(高校数学でいう「微分」は常微分と呼ばれる) 偏微分
- テイラー展開の知識 テイラー展開
- 古典力学の知識 力学
- 熱力学の基礎知識 熱力学
以上が用意できた方はこのページに沿ってやってみましょう!
「何も知らない」、「何から勉強したらいいか全くわからない」という方は、「関数って一体何者?」という問いかけから微分を勉強してみるといいと思います。
音の定義と音速の導出[編集]
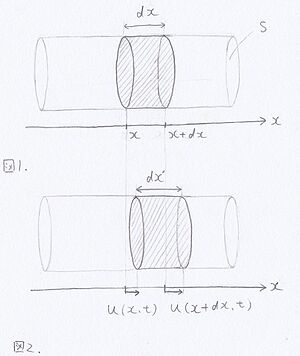
図1のように、断面積が の円柱状の領域について、この領域がある物質(弾性体)で満たされていて、この領域の側面で物質の出入りがないような状況を考える。
の円柱状の領域について、この領域がある物質(弾性体)で満たされていて、この領域の側面で物質の出入りがないような状況を考える。
この領域内の物質に密度の偏りがないとき、図1の斜線部のような部分にある物質の質量を とおくと、この部分は体積が
とおくと、この部分は体積が であるから、このときのこの部分の質量密度は
であるから、このときのこの部分の質量密度は
 …(1)
…(1)
である。さて、図1の状況から 軸方向に物質がわずかに移動して物質に密度の偏りが出来たとき、図1の斜線部分が図2の斜線部分のように変化したとき、変化後の斜線部分の幅
軸方向に物質がわずかに移動して物質に密度の偏りが出来たとき、図1の斜線部分が図2の斜線部分のように変化したとき、変化後の斜線部分の幅 を求める。斜線部分の両端の変位を図1の状況での位置
を求める。斜線部分の両端の変位を図1の状況での位置 と時刻
と時刻 の関数として
の関数として と表わすと、
と表わすと、

となる。ここから

と式変形できる。ここで、 が微小量だとすると、偏微分の定義から
が微小量だとすると、偏微分の定義から
 …(2)
…(2)
となる。また、このとき斜線部分の質量密度は …(3) である。(3)に(2)を代入すると、
…(3) である。(3)に(2)を代入すると、
 …(4) となる。また、
…(4) となる。また、 が位置
が位置 と時刻
と時刻 の関数なので、(4)が成り立つなら質量密度
の関数なので、(4)が成り立つなら質量密度 も
も
 …(5) と表わせる
…(5) と表わせる
(4)に(1)を代入して整理すると、
 …(6) となる。
…(6) となる。
ここで、 を
を のまわりでテイラー展開すると、
のまわりでテイラー展開すると、

となる。ここで、 が1より充分小さいと仮定すると、
が1より充分小さいと仮定すると、
 …(7) と近似できる。(6)に(7)を代入すると、
…(7) と近似できる。(6)に(7)を代入すると、
 となる。両辺を
となる。両辺を で偏微分すると、
で偏微分すると、
 …(8) と表わせることがわかる。
…(8) と表わせることがわかる。
ここで、この状況を力学的な視点で考察しよう。今扱っている物質の性質として、圧力 が質量密度
が質量密度 の関数として、
の関数として、 と表わせると仮定すると、ここに(5)を代入すると、
と表わせると仮定すると、ここに(5)を代入すると、
 と表わせることもわかる。
と表わせることもわかる。
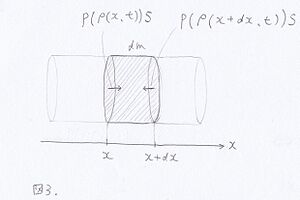
さて、質量が であるような微小部分についての運動方程式は、この微小部分の加速度が
であるような微小部分についての運動方程式は、この微小部分の加速度が と表わせることと、図3のような力が掛かっていることから、
と表わせることと、図3のような力が掛かっていることから、
 …(9)
…(9)
とわかる。ここに(1)を代入すると、

となる。よって

となる。さらに、

と式変形できる。ここで微分の定義より、
 …(10)
…(10)
と表わせることがわかる。(10)に(8)を代入して整理すると、
 …(11)
…(11)
となる。(11)のような形の方程式は一次元の波動方程式と呼ばれていて、この一般解は
 (ただし、
(ただし、 の関数形は任意)
の関数形は任意)
である。これは、 は関数形が変化せずに
は関数形が変化せずに 軸正の向きと負の向きに速さ
軸正の向きと負の向きに速さ で伝わる関数の和で表せることを意味している。
で伝わる関数の和で表せることを意味している。
これは波の定義を満たしている。この波を音と定義する。
空気中の音速[編集]
ここまで考えてきた「物質」が理想気体として扱えるような気体だとしたら、音の速さはどのように計算できるだろうか。熱力学を用いて考えてみよう。
その気体中の音の速さが気体中の熱伝導の速さよりも充分大きいと仮定すると、音によって気体の微小部分は断熱変化すると考えることができる。
その気体の定圧比熱を 、定積比熱を
、定積比熱を として、比熱比
として、比熱比 を用いて微小部分における圧力
を用いて微小部分における圧力 と微小部分の体積
と微小部分の体積 の関係式は
の関係式は
 …(12)
…(12)
と表わせる。これは熱力学から導かれたポアソンの公式である。また、この気体の平均分子量を とし、この微小部分に含まれる気体の物質量を
とし、この微小部分に含まれる気体の物質量を とおくと、この気体の質量密度
とおくと、この気体の質量密度 は
は
 …(13) と表わせる。よって、
…(13) と表わせる。よって、
 …(14) といえる。(14)を(12)に代入して整理すると、
…(14) といえる。(14)を(12)に代入して整理すると、
 …(15) となる。両辺を
…(15) となる。両辺を で微分すると、
で微分すると、
 となる。式変形すると、
となる。式変形すると、
 …(16) となる。(16)に(15)を代入すると、
…(16) となる。(16)に(15)を代入すると、
 …(17) と表わせる。また、気体定数を
…(17) と表わせる。また、気体定数を とし、この気体の温度を
とし、この気体の温度を とすると、この気体の状態方程式は
とすると、この気体の状態方程式は
 である。式変形すると
である。式変形すると
 …(18) となる。(17)に(13)と(18)を代入すると、
…(18) となる。(17)に(13)と(18)を代入すると、
 となる。整理すると、
となる。整理すると、
 となる。
となる。
前節で が音の速さであるとわかっているので、
が音の速さであるとわかっているので、
 が空気中の音の速さである。
が空気中の音の速さである。
この式に、比熱比 (一般的な組成の空気の比熱比)、気体定数
(一般的な組成の空気の比熱比)、気体定数 、温度
、温度 (20℃) 、分子量
(20℃) 、分子量 を代入すると、音の速さは344m/sとわかる。これは同じ条件での音速の実測値と非常に近い値である。
を代入すると、音の速さは344m/sとわかる。これは同じ条件での音速の実測値と非常に近い値である。
日常的に使いやすい音速の近似式としては、気温を とおくと、常温(
とおくと、常温( 、つまり20℃)に近い値において、
、つまり20℃)に近い値において、

 と表すことができる。
と表すことができる。